多 角形 角度 702122

首先，假定我们有两条已知直线 ，他们的"零界线"为 ，在直角坐标系下画出他们的图形，我们可以很容易看出角的朝向： 如图，这个例子中紫线为"零界线"，按 函数的定义，可以得出 表示的图形在"小"字的一侧，即一个顶点在原点，开口向第四象限的角。 通过平移，我们也可以得到更为一般的角方程。 （二）三角形方程 角方程的构造中，我们采用的是 （ (8 版权 "角度和法"的思路是：多边形内的点，与所有顶点顺次连接形成向量的夹角之和为2π。 图例说明，如下图所示： O点在多边形之内，其与多边形所有顶点的连线，组成6个向量，顺次形成6个向量夹角，显而易见，这6个夹角之和为2π。 P点在多边形之外，其与多边形所有顶点的连线，组成6个向量，顺次形成6个向量夹角，显而易见，这6个夹角之和不等于2π多边形网格处理 答辩人：周航 保角：当第一基本型是单位矩阵的倍数或者奇异值相同的时候，向量的角度得到了保留。 保面：第一基本型行列式值 1或者所有奇异值相乘值 1时，圆形面积在变换后不变。 等距：第一基本型是单位矩阵或者奇异值 1。 求解方法：① 格林—拉格朗日变形张量法 ②

正多边形 属性

多 角形 角度

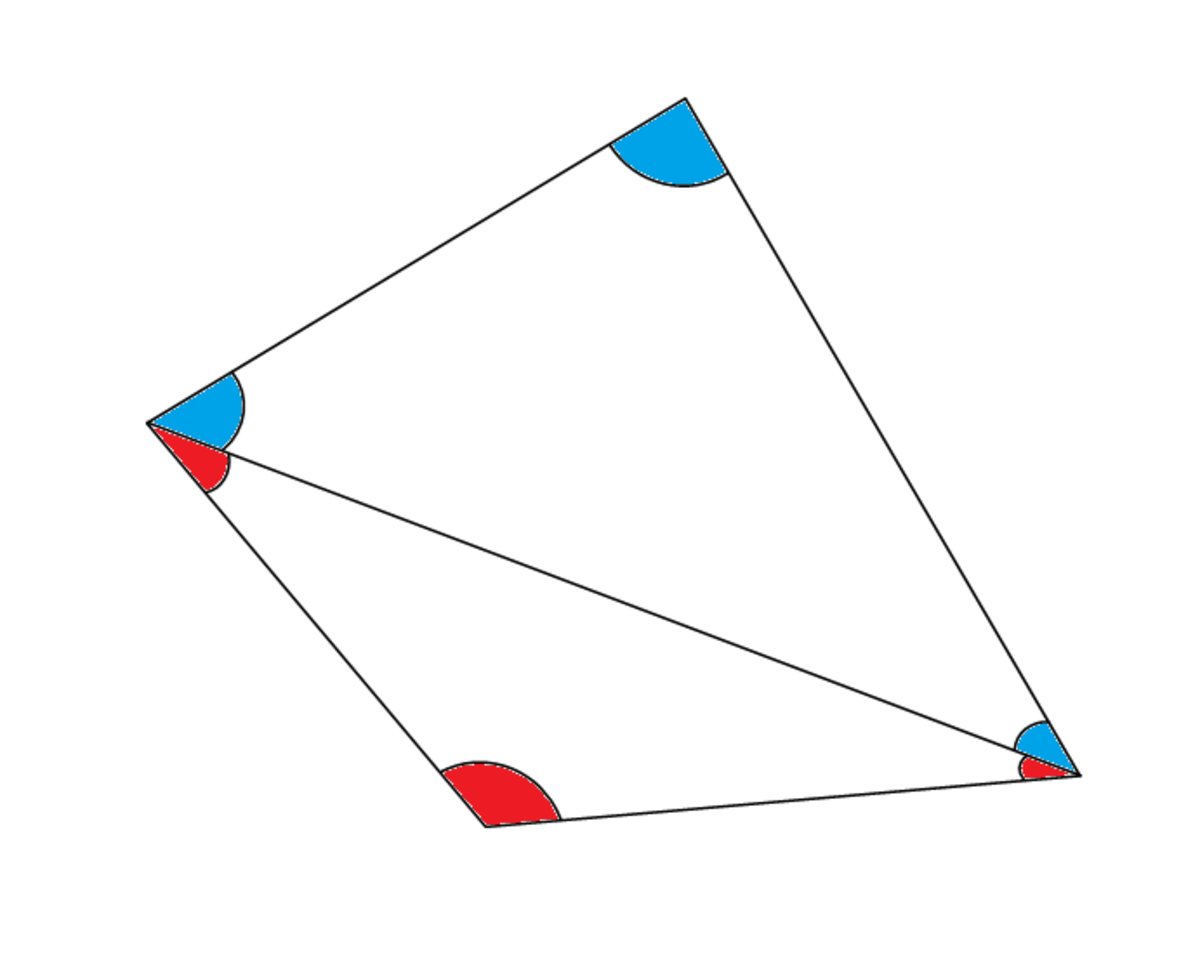
多 角形 角度-美国公共大学：几何学 本课程共37集 翻译完 欢迎学习 讲师：VA 学院介绍：美国公共大学（APUS），前身为美国军事大学，02年改组，现为全世界超过五万人开放远程教育课程，提供在教育、技术、商业管理、人文艺术、国家安全、军事学习、情报工作、国土多边形的内角和三角形的内角和等于180°；正方形、长方形的内角和等于360°那么，任意一个四边形的内角和是否也等于360°呢？探究在四边形abcd中，你能利用三角形内角和定理证明四边形内角和等于360°吗？adcb则四边形abcd被分为两个三角形， abc和 acd所以，四边形abcd的内角和= abc的内角

回报与许多参差不齐的角度的3d摘要浅粉红色的多角形背景非常突出库存例证 插画包括有

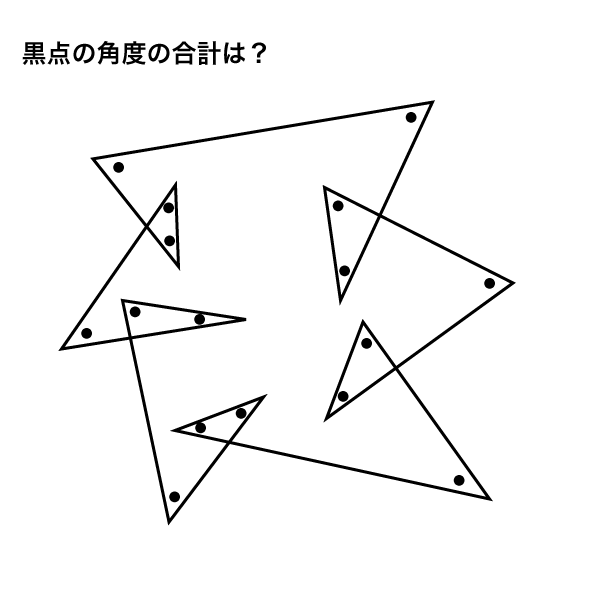
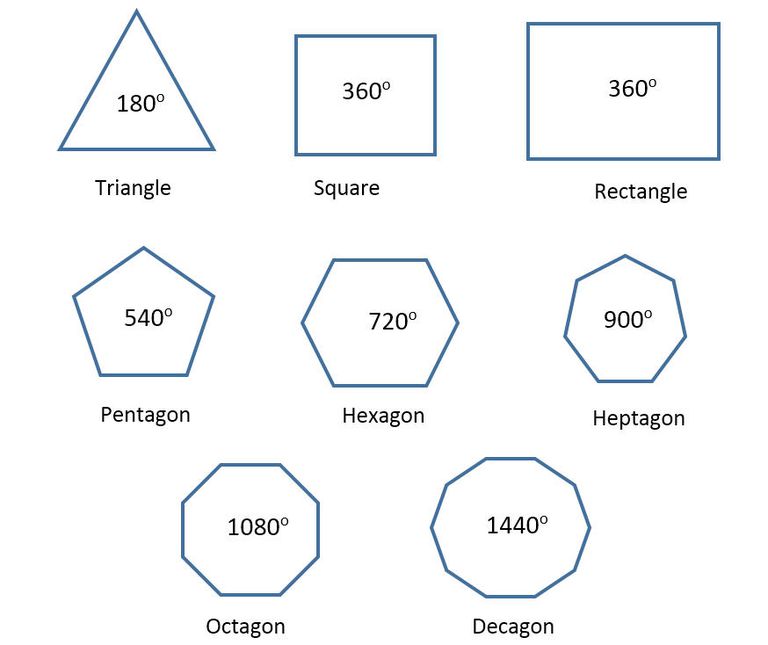
 最小外接矩形的四个边都与轮廓相交，该矩形的旋转角度与轮廓的形状有关，多数情况下矩形的四个边不与图像的两个轴平行。minAreaRect()函数可以求取轮廓的最小外接矩形，该函数的函数原型在代码清单7中给出。 代码清单7 minAreaRect()函数原型 RotatedRect cvminAreaRect(InputArray points) points：输入的2D多边形内角和公式 设多边形的边数为 n 则其内角和＝（n－2）*180° 因为 n 个顶点的 n 个外角和 n 个内角的和 ＝n*180° （每个顶点的一个外角和相邻的内角互补） 所以 n 边形的外角和 ＝n*180° －（n－2）*180° ＝n*180° －n*180° ＋360° ＝360° 即 n 边形的外角和等于 360° 设多边形的边数为 n一些常见的多边形内角总度数如下： 三角形（三边多边形）的内角总和为180度。 四边形（四边多边形）的内角总和为360度。 五边形（五边多边形）的内角总和为540度。 六边形（六边多边形）的内角总

直角三角形计算 直角三角形在线计算器 请在下面输入数值 (图形在下面) a垂直边长 b底边长 c斜边长 A角度 B角度 C角度 文章目录Thiessen多边形(Voronoi图)类型点的Voronoi图线与面Voronoi图例子：求解相邻最近和最远的点rnThiessen多边形(Voronoi图)rn来源1911 年荷兰气候学家AHThiessen为提高大面积气象预报的准确度,应用Voronoi 图对气象观测站进行了有效区域划分。故在二维空间中,Voronoi 图也称为泰森( Thiessen) 多边形。rnTan x° = 对边/邻边 = 300/400 = 075 tan1 of 075 = 369° （保留一位小数）

1 角度制（ Degree Measure） 把一个圆周平均分成360份，其中的每一份都是1 o 的角。 这种以"度"作为单位来度量角度单位制叫做角度制。 下图是我们常见的180 o 角度尺 Protractor 。 2 弧度制（ Radian Measure） 长度为半径长的弧，所对的圆心角是 1 弧度 （Radian），用符号 rad 表示。 正角度弧度数是一个正数，负角度弧度数是一个负数，零角度弧度数。 判断一个点是否在多边形内有几种不同的思路，相应的方法有： 射线法 ：从判断点向某个统一方向作射线，依交点个数的奇偶判断； 转角法 ：按照多边形顶点逆时针顺序，根据顶点和判断点连线的方向正负（设定角度逆时针为正）求和判断； 夹角和法 ：求 既然是和面法线有关系， 我们在Display显示菜单下，在多边形 所以面法线的夹角就为0度，而0度

八边形 维基百科 自由的百科全书

多边形中的角度加起来是什么猫头鹰 1jdc金宝搏

 多边形 (Polygon)： 由三条以上的直线所组成的形状为 多边形 。 凸多边形 (Convex Polygon)每个内角 (Interior Angle)都是锐角 (Acute Angle)或钝角 (Obtuse Angle),也就是没有大于180°的优角 (Reflexive Angle)搜索的 多边形 。 凹多边形 (Concave Polygon)至少有一个优角 (Reflexive Angle)的 多边 ©️21 CSDN 皮肤主题 大白 设计师CSDN官方博客 返回首页多边形角度 ：指定将要绘制或置入的多边形相对于画布的角度。 边角类型 ：指定多边形所需要的边角类型（圆角、反向圆角或倒角） 多边形半径 ：指定所绘制的多边形的精确半径。使用屏幕上的 构件 可 修改半径。 多边形边长度 ：指定多边形每一边的长度。然后选择任意一点为多边形的起点，然后根据需要选择下一点，可以在命令行选择绘制多边形的长度、角度、圆弧等，同时输入需要的长度、角度。最后，按回车键完成绘制。 你看这样不就将不规则的多边形在cad中绘制完成啦！操作起来很容易的，相信大家都会轻易完成的！ 评论 取消 评论 最新

单开关方形磁铁开 关多角度fm2焊接磁性固定器固定器可切换六角形焊接磁铁 Buy 焊接磁铁集 磁体焊接支架 定位器焊接磁铁

N邊形內角和定理 Youtube

计算区域面积 计算边界框 计算边界等效多边形 计算两点间角度 计算绝对中心点 计算多边形质心 计算顶点平均值质心 根据点、距离和角度计算目标点 计算两点间距离 计算角度闭合差，闭合导线由多边折线构成多边形。因此可求出多边形内角和为∑β理=（n2)x180° 为多边形角度理论值 4 计算坐标方位角，计算方位角时，通过大致导线图判断观测角方向，若为左角 α前=α后180°β左 右角计算为：α前=α后180°β右。若在计算时方位角超过360°应减去360°或若干个360 多边形的内角和公式是什么 文/宋则贤 多边形内角和的计算公式为（N2）×180，其中N为多边形的边数。在平面多边形中，边数相等的凸多边形和凹多边形内角和相等。 多边形的内角和公式 1、多边形的内角和等于（N2）x180；

中2数学 複雑な多角形 角の和 応用問題

多角形の内角の和 は何度なのか を説明します おかわりドリル

 为了方便绘制，我们计划所有的正多边形统一从坐标系中的某个点出发，譬如坐标系中的点E｛x=0,y=R｝。 在scratch中，我们每次绘制一个正多边形的时候，都要将位置移动到 {0,R}这个点，然后面朝某个方向开始绘制。 而对于正Num边形来说，这里我们取Num=6，也 一 轮廓检测 在计算机视觉中，轮廓检测是另一个比较重要的任务，不单是用来检测图像或者视频帧中物体的轮廓，而且还有其他操作与轮廓检测相关。这些操作中，计算多边形边界，形状逼近和计算机感 兴趣区域。这是与角度 a = 角度 角度 b = 角度 角度 c = 角度 周长 = 单位 面积 = 单位/平方 内径 = 单位 外接圆半径= 单位

內角和外角 维基百科 自由的百科全书

5角形角度 シモネタ

有个思路，先把多边形三角剖分，变成一堆三角形的组合，然后可以判断点是否在各个三角形内。 （其实三角剖分应该算是解决方案的重点，可以用earclipping三角剖分）。 然后判断点在三角形内又可以先算出点的双线性插值坐标（s,t） P＝AsV1＋tV2，注意到在P,A,V1,V2都已知的时侯这是个二元一次方程，用克拉默法则一步到位解出（s,t），注意三点不可以共线不然行列式为0直角三角形计算器 如果给出足够的几何属性， 直角三角形计算器 就能自动补全直角三角形的所有属性，如面积，周长，边和角度。 直角三角形是一个具有三个顶点（角）和三个边（边）的多边形，其中两条边以直角相交。 直角三角形 维基百科页面⊇ ⊇ ⊇ 依照03版本的PPT展示不规则多边形体如何绘制及填充内部1、选定插入位置在上方工具栏里面依次点击插入图片自选图形2、在自选工具第一个里面,点选"任意多边形"3、根据需要手工画出需要的多边形,记住要封闭起来4、画完后,选中

多角形图片 多角形素材图片大全 摄图网

Sdime Ntnu Edu Tw

如果给出足够的几何属性，任意三角形计算器就能自动补全任意三角形的所有属性，例如面积，周长，边和角度。 三角形是具有三个顶点（角）和三条边（边）的多边形。 任意三角形 维基百科页面相关计算器：等边三角形计算器等腰三角形计算器直角三角形计算器分离轴定理（Separating Axis Theorem） 概念：通过判断任意两个 凸多边形 在任意角度下的投影是否均存在重叠，来判断是否发生碰撞。 若在某一角度光源下，两物体的投影存在间隙，则为不碰撞，否则为发生碰撞。 注意： 分离轴定理只适合 凸多边形 ，所以如果是 凹多边形 的话需要转换成多个 凸多边形, 具体转换算法参考git上 https// githubcom/schteppe/pol ydecompjs 用于将1 在工具箱中单击"多边形工具"，按住Ctrl键在页面上拖拽绘制一个正多边形。 2 在多边形选中状态下，单击菜单栏"窗口>泊坞窗>圆角/扇形角/倒菱角"命令，界面右侧弹出"圆角/扇形角/倒菱角"面板。默认为"圆角"类型，根据图形大小设置半径数值，作图窗口会根据您设置半径的变化实时预览，如图所示。

回报与许多参差不齐的角度的3d摘要浅粉红色的多角形背景非常突出库存例证 插画包括有

七边形 搜狗百科

在上图中，左圆柱体具有基本的平面着色，并且每个多边形根据其与光源的相对角度进行着色。每个多边形上的光照在多边形区域内保持恒定，因为该表面是平坦的。以下是显示了线框网格的同样两个圆柱体： 两个 12 面圆柱体，左侧带有平面着色，右侧带有平滑着色 右侧的模型与左侧的模型具有 本文讨论如何判断一个点是在多边形内部，边上还是在外部。 为了方便，这里的多边形默认为有向多边形，规定沿多边形的正向，边的左侧为多边形的内侧域，即多边形边按逆时针方向遍历，不考虑自交等复杂情况。 比较常见的判断点与多边形关系的算法有射线法、面积法、点线判断法和弧长法等，算法复杂度都为O (n)，不过只有射线法可以正确用于凹多边形 多边形 实现任意条边的多边形，大家思考一下都会知道如何实现，平均角度=360度／边数，不是吗？ 在知道中点和第一个顶点的情况下，第n个顶点与中点的角度 = n*平均角度；然后记录下每个顶点的位置，然后依次绘制每个顶点的连线即可。这里用到了二维旋转

正多边形 属性

多角形の内角の和 は何度なのか を説明します おかわりドリル

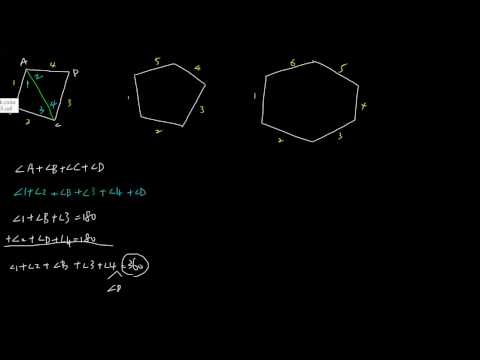
 1一些常见的多边形内角总度数如下： 三角形（三边多边形）的内角总和为180度。 四边形（四边多边形）的内角总和为360度。 五边形（五边多边形）的内角总和为540度。 六边形（六边多边形）的内角总和为7度。 八边形（八边多边形）的内角总和为1080度。首先打开cad，在界面下方右键单击极轴追踪图标，选择设置。 2/4 在弹出的草图设置中勾选启用极轴追踪，然后在附加角中点击新建，输入想要追踪的角度，这里小编新建0度和30度，最后确定。 CAD迷你画图CAD制图初学入门必备 广告 3/4 设置完极轴追踪之后，我们在画线的时候每隔30度就会出极轴，很容易就画出了角度，画其它角度的设置方法都是一样的。 广告 琵琶正多边形内角和定理n边形的内角的和等于： （n － 2）×180° (n大于等于3且n为整数）。 证法一：连结多边形的任一顶点A1与其不相邻的各个顶点的线段，把n边形分成（n2）个三角形 因为这（n2）个三角形的内角和都等于（n2）·180°（n为边数） 所以n边形的内角和是（n2）×180° 证法二：在n边形的任意一边上任取一点P，连结P点与其不相邻的其它各顶点的线段可以把n边形

多边形中的角度加起来是什么猫头鹰 1jdc金宝搏

七边形是七角度多角形摘要七边形几何商标象向量例证 插画包括有装饰 平面 投反对票 多角形

多邊形與內角和 四年級數學 Grade 4 Math Sum Of Interior Angle Of Polygon Youtube

複雑な多角形の角度の和が知りたいのですが 添付画像の１６か所の黒丸部分の Okwave

內角和外角 维基百科 自由的百科全书

什么是江恩六角形 赢家财富网

Studydoctor多角形の角度の問題 中２数学 Studydoctor

觀念 任意三角形三內角和等於180 度的證明1 已下架內容 均一教育平台

角度を求める 凸型多角形 Next Stageのブログ

多邊形外角和多邊形的內角公式和多邊形外角和的簡單證明方法 Yihbk

二次元裂縫 數學 多邊形的內角合

303 8多角形求法與畫法 拙園創意木工 隨意窩xuite日誌

如何计算角度 8 步骤 包含图片

N邊形內角和定理 已下架內容 均一教育平台

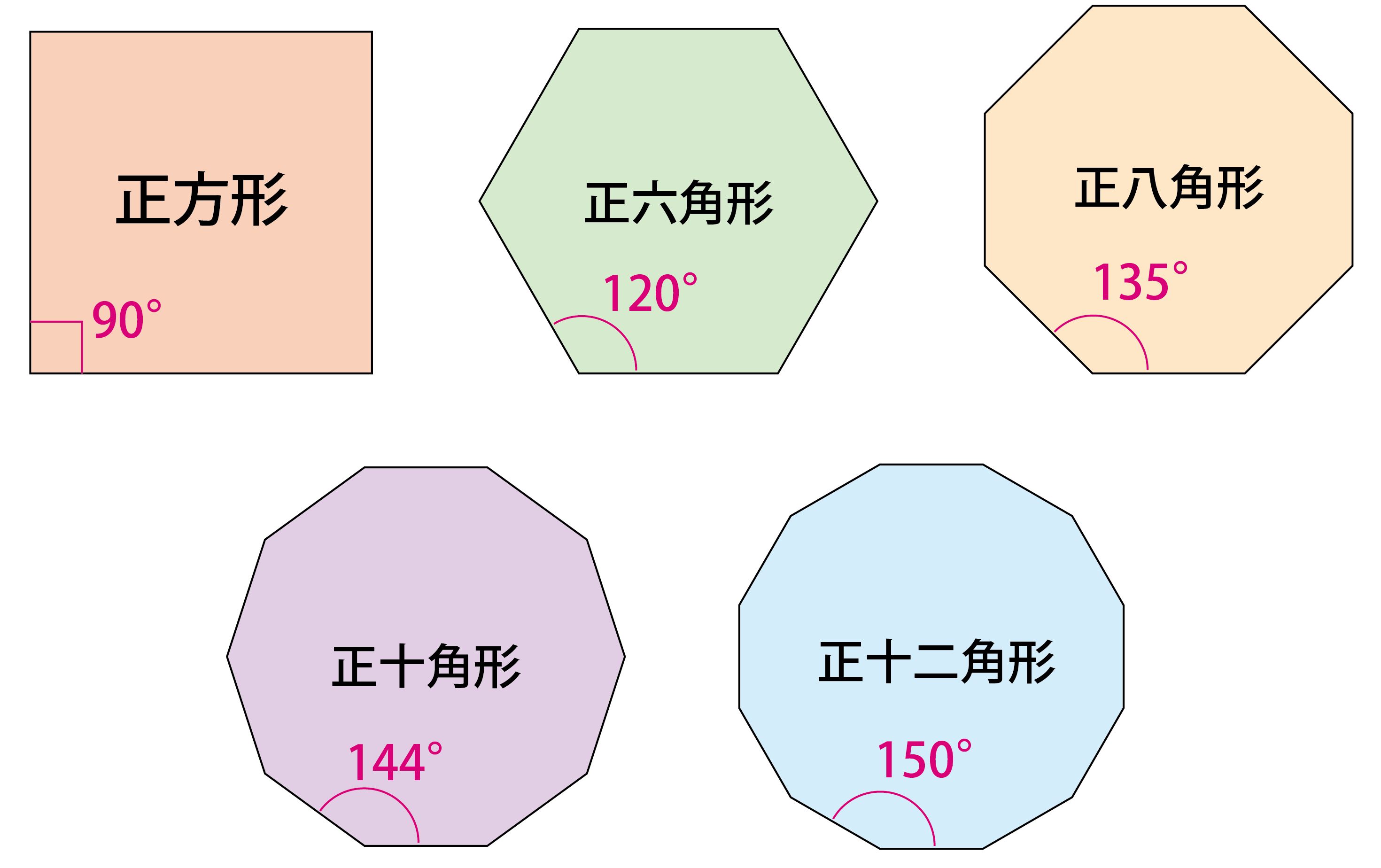
多角形の角度と組み合わせに関する問題 熊本県共通 21年 恋する中高一貫校 適性検査 徹底攻略

多角形の内角の和の公式と外角の和を利用した角度の求め方

正八边形的角度是多少 请问正八边形可以用三角形组成 每个三角形的三边和角度是多少 三人行教育网 Www 3rxing Org

中２数学 平行線と角度 内角外角 多角形 角度 Youtube

高中數學知識點 多邊形外角和等於360 動畫版 每日頭條

觀念 任意三角形三內角和等於180 度的證明1 已下架內容 均一教育平台

多角度专业视频素材模板大全 新视界多角度专业实拍视频素材库

多角形滤网连续男性剪影抽象人赛跑者低多背景传染媒介例证向量例证 插画包括有抽象 马拉松

多角形の角 無料で使える中学学習プリント

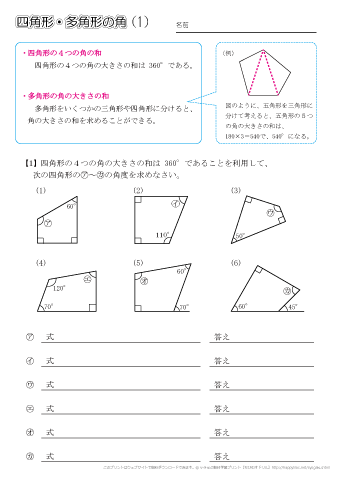
小学５年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生

多角形の内角の和の求め方をイチから解説するぞ 中学数学 理科の学習まとめサイト

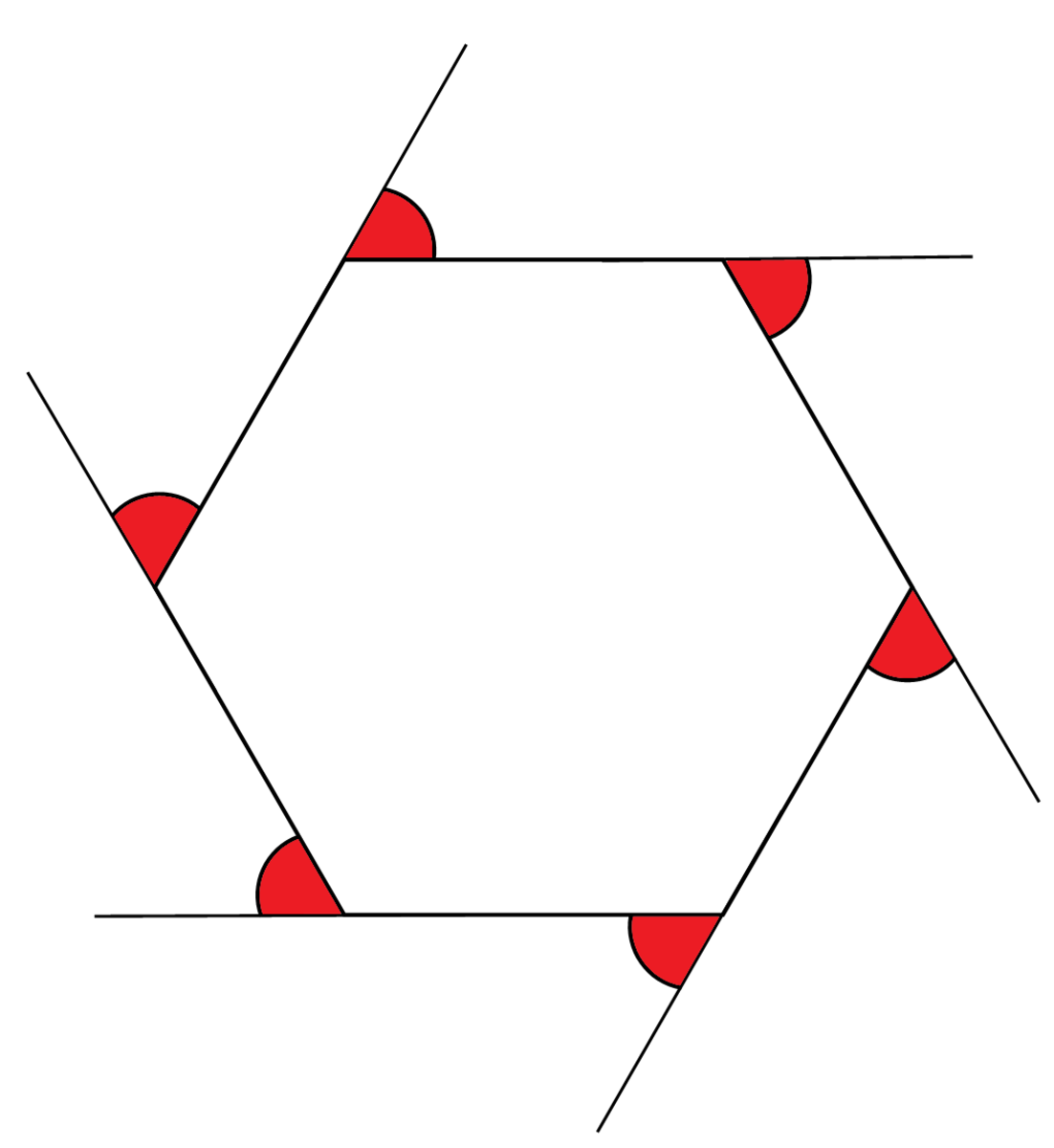
多边形中的角度加起来是什么猫头鹰 1jdc金宝搏

コンプリート 多角形角度公式 ニスヌーピー壁紙

内角の和から多角形を求める方法と一覧表 具体例で学ぶ数学

中2数学 正多角形の外角の大きさが3秒でわかる公式 Qikeru 学びを楽しくわかりやすく

多角形 の内角の角度 計算ドリル 問題集 数学fun

小５算数 四角形 多角形の角度 Youtube

正多邊形 定義 相關概念 外接圓 內切圓 內角 外角 中心角 面積 對稱軸 鑲嵌規 中文百科全書

定制电焊神器辅助工具焊接神器固定强磁焊工直角焊接定位器多功能磁力定做六角形小号25lbs 吸附力12kg 图片价格品牌报价 京东

正多邊形的內角與外角 Live 多媒體數學觀念典online

正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく

多角形 四角形 五角形 六角形 の内角の和の公式 問題の解き方 数学fun

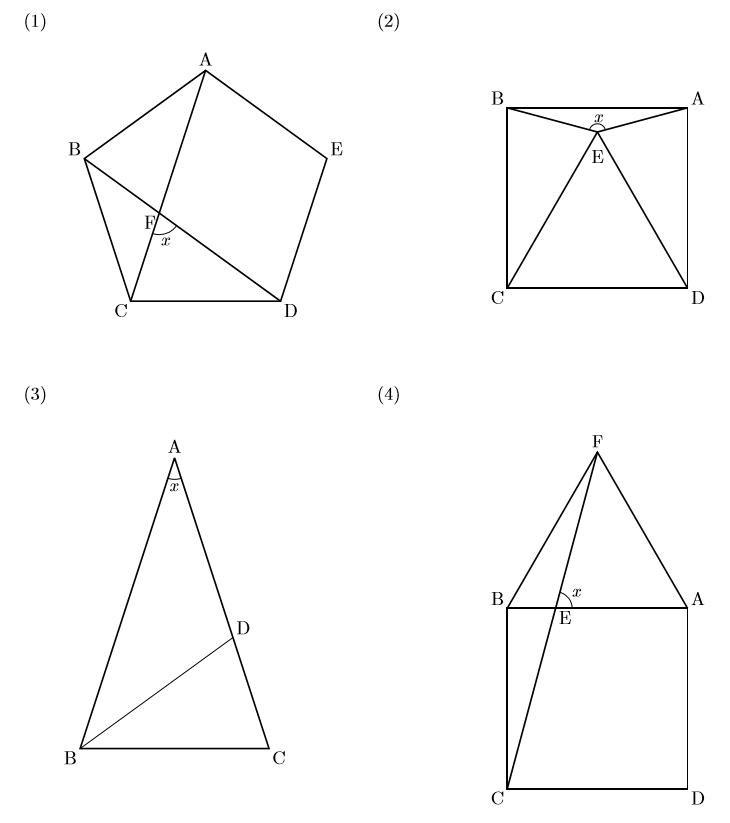
中学数学 中2角度の問題 多角形 数樂管理人のブログ

多角形の角度の和の求め方 添付画像の黒い印の角の角度の和を求めたい 数学 教えて Goo

不同 放置 三角形 颜色 形状 角度 更多 3d Canstock

益智城 數學教具 畫圓工具 畫圓尺 多功能繪圓器 圓尺 可畫各種半徑圓 多角形及角度的標示圓弧 蝦皮購物

上6 角形五角形角度 シモネタ

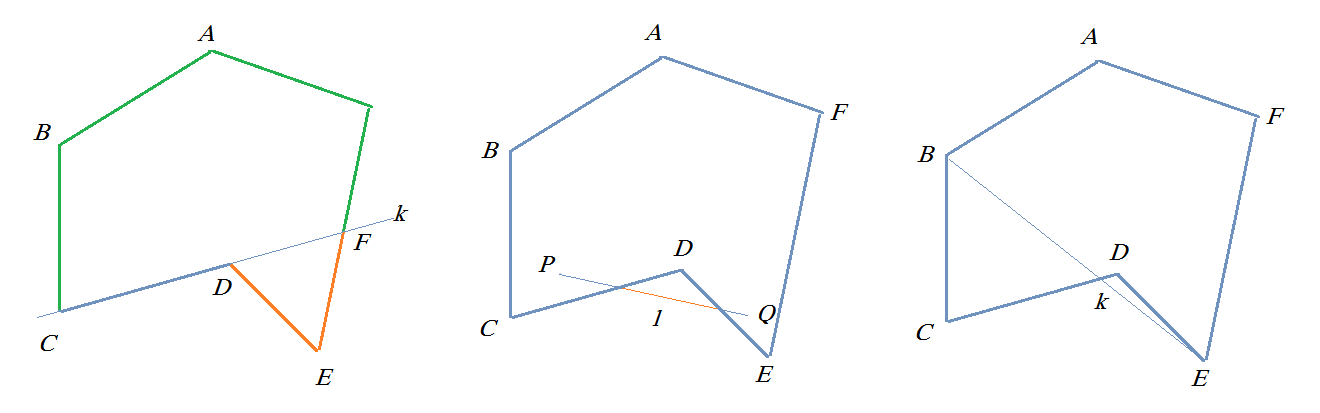
凹多邊形 定義 示例 性質 判斷 中文百科全書

多邊形內角和公式三角形內角的奧祕 rbmi

多邊形幾何 五角形 六邊形和十二邊形

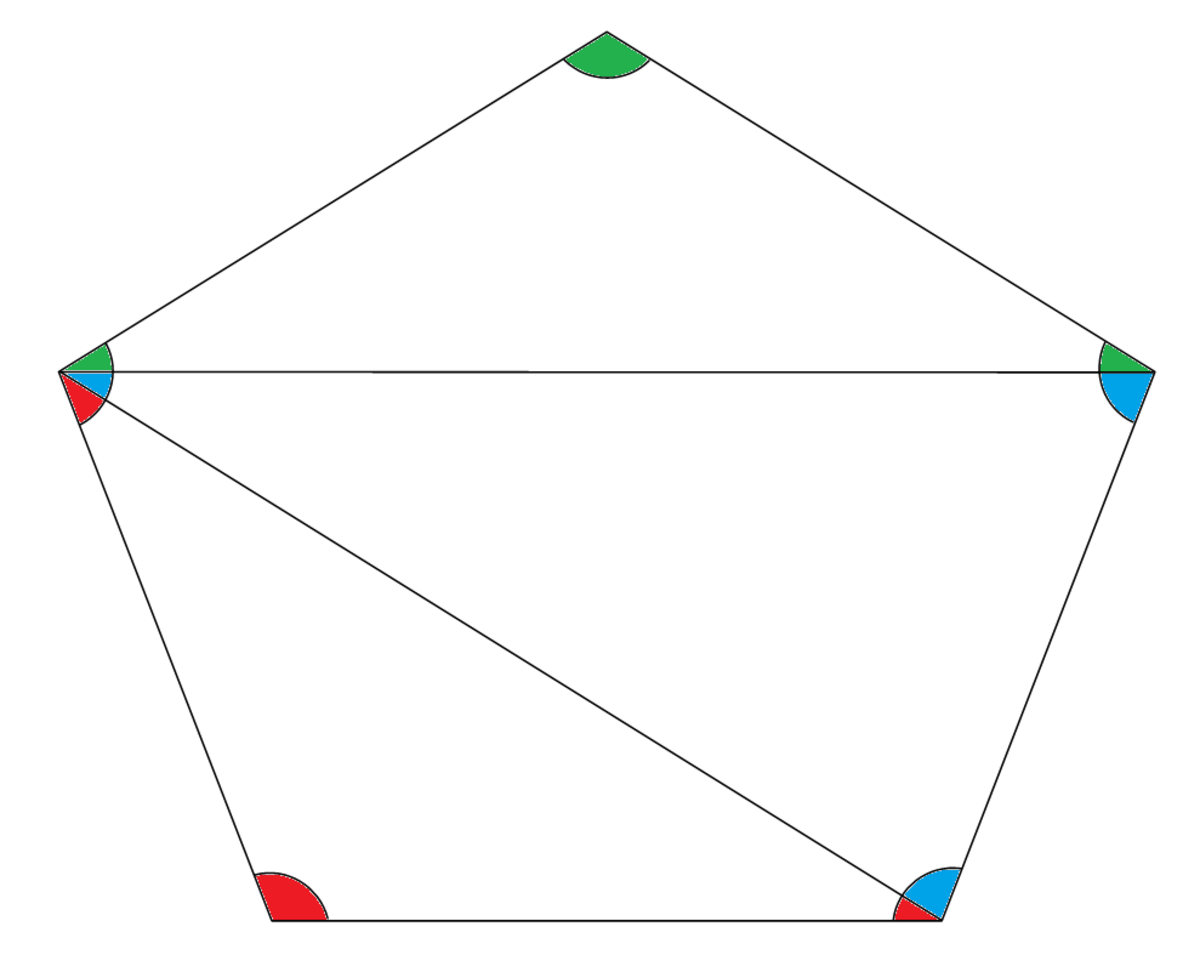
多边形中的角度加起来是什么猫头鹰 1jdc金宝搏

1

多角形の内角の和の公式を３通りの方法で証明する 具体例で学ぶ数学

正多角形の内角と中心角 家紋の描き方007b 夏貸文庫

3分で分かる 多角形の内角の和の求め方 公式の証明などをわかりやすく 合格サプリ

1

縫紉王 多角度透明拼布尺60度三角拼布尺六角形拼布尺45度菱形拼布尺60度菱形拼布尺鑽石梯形壓克力尺

多角形の性質 中学受験準備のための学習ドリル

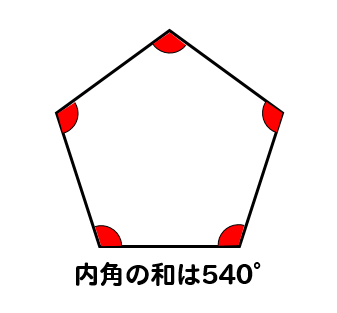
正多角形の1つの内角 外角を求める方法を問題解説 数スタ

八边形 维基百科 自由的百科全书

1

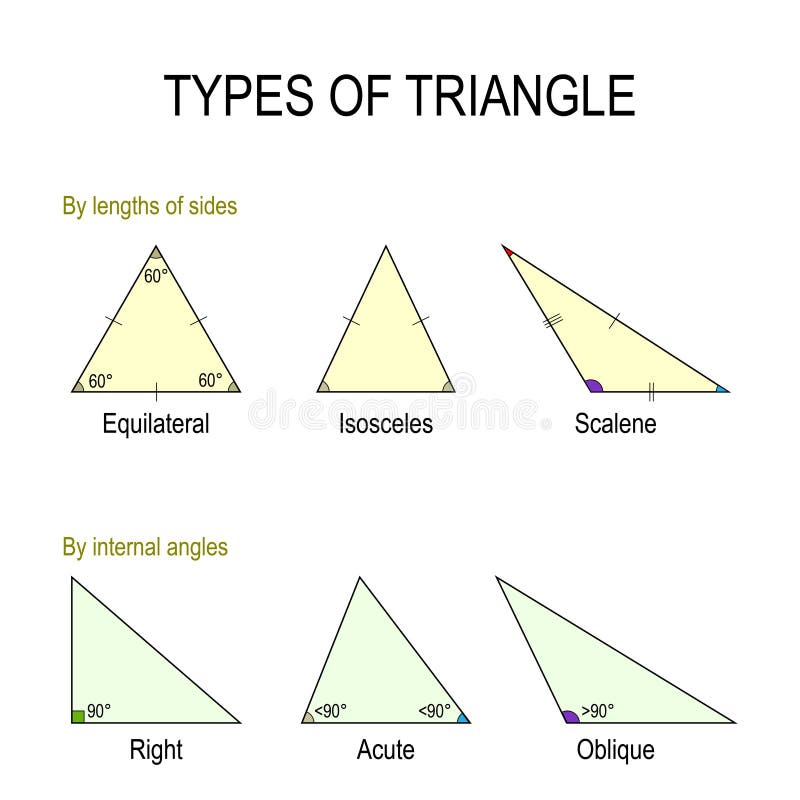
三角的类型向量例证 插画包括有多角形 类型 内部 学校 角度 例证 几何 奥布斯

補角補角的意思 Mrsysy

例題 直角三角形內角的基本計算題1 數學 均一教育平台

正多角形の内角を4秒で計算できる公式 Qikeru 学びを楽しくわかりやすく

例題 任意三角形內角計算的基本題型 數學 均一教育平台

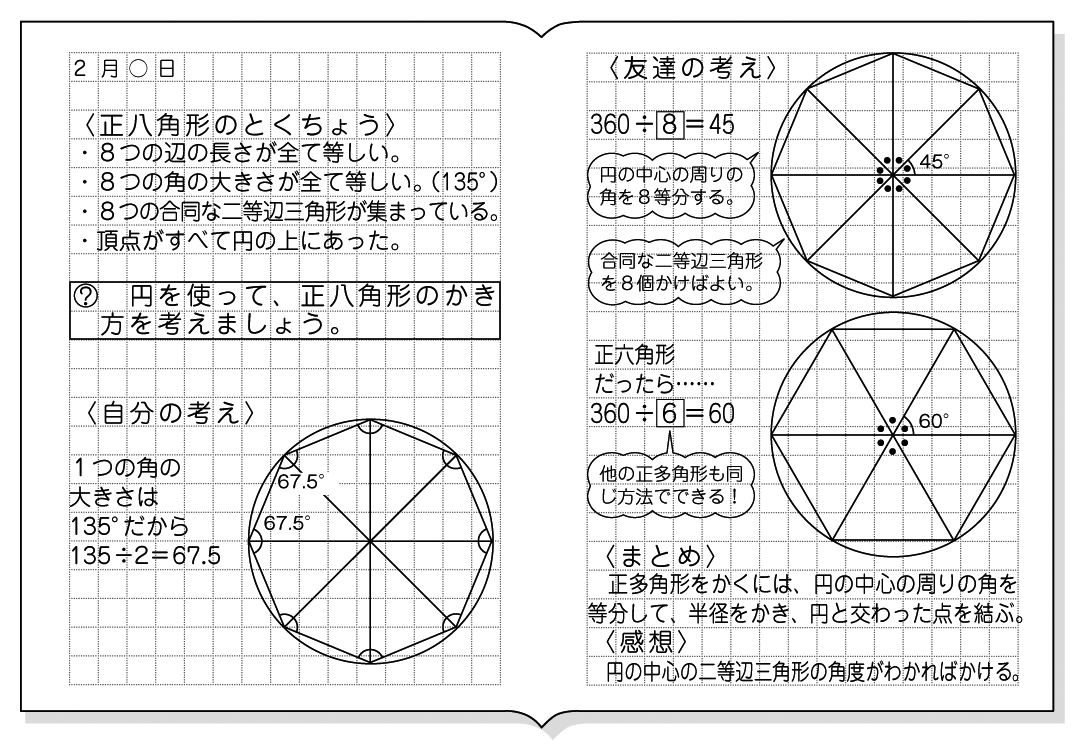
小5算数 正多角形と円 指導アイデア みんなの教育技術

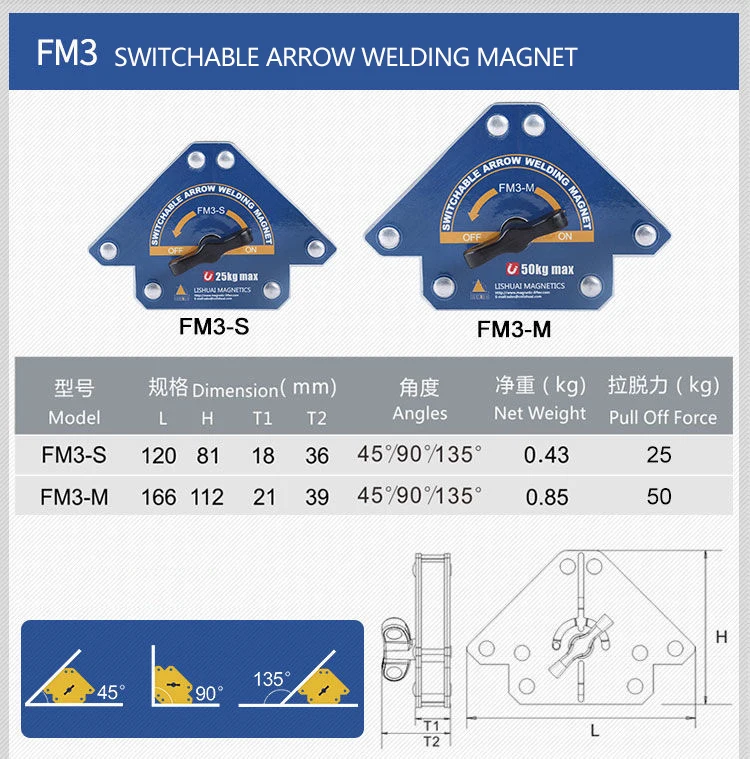
单开关方形磁铁开 关多角度fm2焊接磁性固定器固定器可切换六角形焊接磁铁 Buy 焊接磁铁集 磁体焊接支架 定位器焊接磁铁

正多边形外角度数公式 扒拉扒拉

画像をダウンロード6角形角度 シモネタ

小５算数 内角の大きさを求めて正多角形を作図しよう ベネッセのプログラミング教育情報

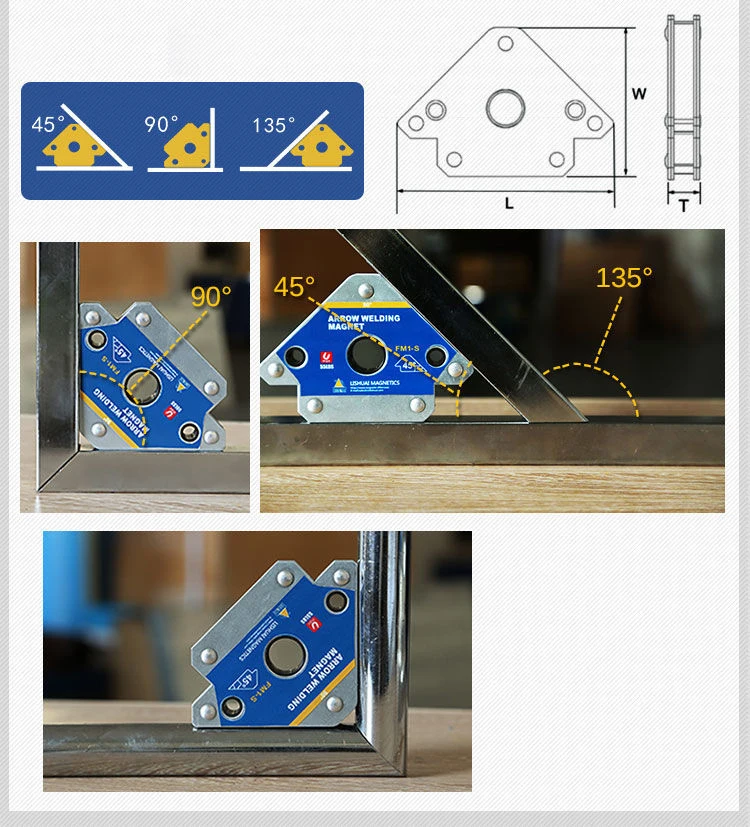
单开关方形磁铁开 关多角度fm2焊接磁性固定器固定器可切换六角形焊接磁铁 Buy 焊接磁铁集 磁体焊接支架 定位器焊接磁铁

簡単公式 五角形の内角の和を3秒で計算できる方法 Qikeru 学びを楽しくわかりやすく

正多角形の角数を大きく増加して行くとその内角は180度に近づく 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ

多边形的内角

1

Ai中正六角形怎么调整大小和角度 Illustrator教程 平面设计 得牛网

角と平行と多角形 わかる数学

多角形とは 外角 内角の和 面積 対角線の本数の公式と求め方 受験辞典

正多边形 维基百科 自由的百科全书

平行四边形 相关京东优惠商品 2 价格图片品牌优惠券 虎窝购

正多邊形內角正多邊形的一些基本概念 Mswju

几何形状的数学定义和分支与点 线 角度 表面和固体的成交在白色backgr 向量例证 插画包括有多角形 要素

江恩六角形的结构 赢家财富网

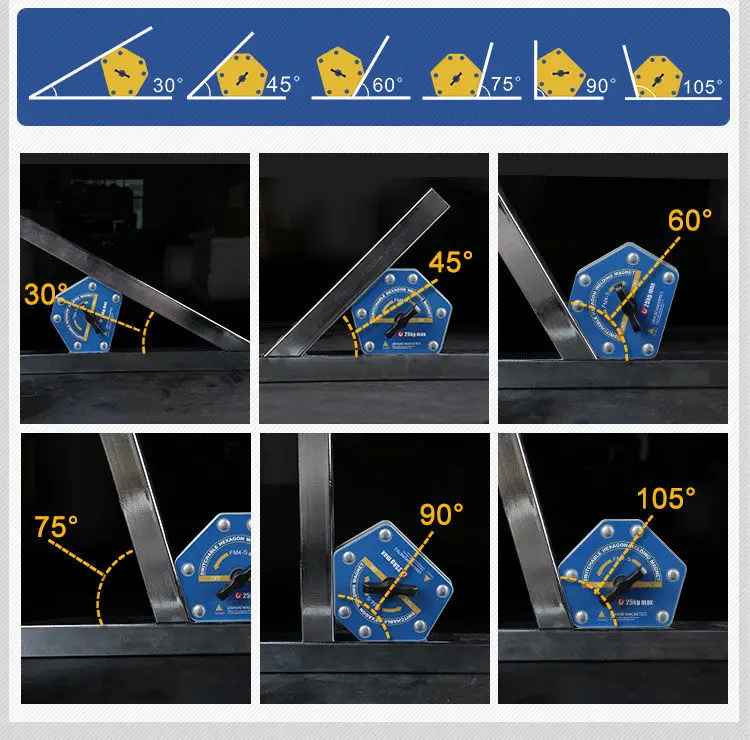
单开关方形磁铁开 关多角度fm2焊接磁性固定器固定器可切换六角形焊接磁铁 Buy 焊接磁铁集 磁体焊接支架 定位器焊接磁铁

多角形の内角の和 算数の公式覚えてますか

如何计算角度 8 步骤 包含图片

初中數學 多邊形的內角和與外角和題型總結 掌握這些就夠了 每日頭條

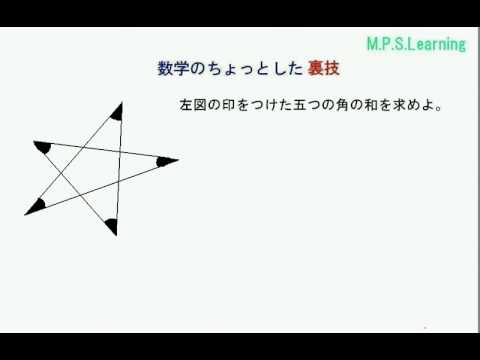
多角形の角度 Youtube

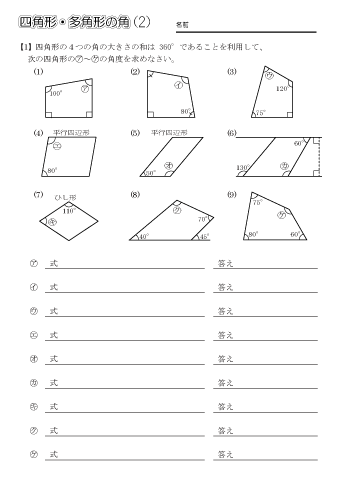
小学５年生の算数 四角形 多角形の角 問題プリント ちびむすドリル 小学生

正ｎ角形の内角の和は2 ｎ 2 直角である 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ

Scratch 3 Scratch Mit Eduprojects Kagoshima Prefectural

多角形の内角の和 外角の和は 正多角形の内角の求め方は 証明や問題をわかりやすく解説 遊ぶ数学

高雄宅速修室內裝修企業有限公司 高雄水電維修工程

正ｎ角形の内角の和は2 ｎ 2 直角である 多面体紙工作で数学を楽しむ 行動の記録 楽天ブログ

Sdime Ntnu Edu Tw