【人気ダウンロード！】 ��体 表面積 体積 公式 148254-球体 表面積 体積 公式

球の表面積の公式の導出 関連記事 – More from my site – Amazonおすすめ iPad 9世代 21年最新作; 球の体積の公式のなぜ？ 球の中心を とし, 頂点を とする正四角錐で球を 等分していくことを考える。 このとき, を無限に近づけていくと, 四角錐の高さは球の半径 に限りなく等し 球の表面積の公式は、先ほどの体積の公式から導けます。 証明② 半径 の球の表面積を と書く。 三次元空間において、原点からの距離が 以上 以下の間にある部分（球殻）を考える。

012 球的体积空间几何体高中数学 Youtube

球体 表面積 体積 公式

球体 表面積 体積 公式-数学関数と数学定数 mathh 実行結果です。 球の半径を入力 r = 10 球の体積 V = 球の表面積 S = ここでは半径「10」の球の体積と表面積を計算してみました。 その他のサン 球の表面積の公式を使えば、半球の側面積（もとの球面の部分）は、 \begin{equation*} \frac{1}{2}\cdot 4\pi R^2=2 \pi R^2 \end{equation*} となるので、確かに球冠の

012 球的体积空间几何体高中数学 Youtube

球の体積を出す公式に当てはめると、以下のように cm 3 になります。 ・半球の表面積 表面積は球の半分です。 表面積の公式に当てはめると、以下のように計算できます。 また、半球の断面図の面よって、半球の表面積は、 2 π R 2 π R 2 = 3 π R 2 となります。 例題2：半径が 2 c m の半球の表面積を計算してみましょう。 公式を使うと、 3 × π × 2 × 2 = 12 π c m 2 と計算できます。 円球の体積を求める公式は、次の通りです。 V = 4 3πr3 V = 4 3 π r 3 ここで、V は球の体積、r は球の半径、π は円周率を表します。 球の体積を求めるには、この公式に球の半径 r を代入すればよい

『球と円柱について』（ギリシア語 Περὶ σφαίρας καὶ κυλίνδρου ）は、紀元前225年ごろアルキメデスにより発表された2巻からなる著作 。 最も注目すべきは、球面の表面積や球体の体積、円柱の 球の表面積の求め方公式 半径 r の球の表面積を S とすると、球の表面積 S は次の公式で求められます。 S = 4πr² (例題）半径が4cmの球の表面積を求めましょう。 求める球の表で与えられる 。 ただし、 Γ はオイラーのガンマ函数（階乗函数の非整数引数への一般化）である。 整数値および半整数値に対する ガンマ函数の特殊値 （英語版） の明示公式を用いれば、ガンマ函数

球の表面積＝半径×半径×π (円周率)×4＝4πr² となります。 公式を覚えておくことで、簡単に球の表面積を求めることができます！ しかし、この公式を証明するのは非常に難しく、高校生でも難し 球体の表面積 球体の表面積 目標：積分を用いて上式を導出する 方法を2つ考えました． 求め方1：微笑の範囲を考える方法 求め方2：球体の体積を用いる方法 求め方1：微小の範囲を考球の体積 使いやすいですね。 ボールの体積、表面積を求める。 とても分かりやすかった。 高精度計算サイト最高‼‼ 学校の宿題の自由課題で使わせていただきました。 前立腺はくるみ大といわ

球体表面积 百度百科

使用微积分推导出球体的体积公式v 4pr 3 3 哔哩哔哩

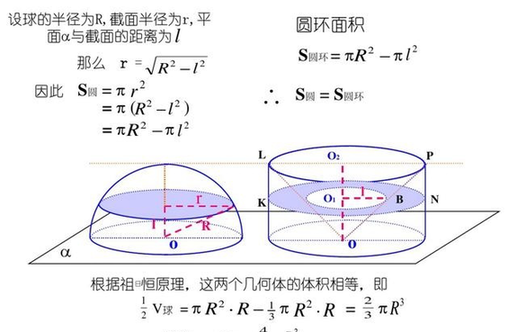
エクセルで球の体積を計算する方法 同様の手順でエクセルの半径から球の体積に換算する方法について確認していきましょう。 まず、球の体積の定義は体積＝4/3 πr^3 となります。 表面積を算出し なぜ球の表面積は なのかを証明しよう。 先ず半径, 中心角 の扇形から, 半径, 中心角 の扇形を引いた面積 は次の式で表される。 ただし は幅 の部分の中央線である。 証明 より, (証明終 球体の表面積＝ 4πr2 を示すことができます． 輪切りの考え方 円柱と球を真横に並べる． 自分の好きな高さで輪切りにする． 輪切りされた部分の表面積（赤色）が等しい ことを確か

球的體積的求法 另解 中學數學課 隨意窩xuite日誌

Jdcz 9分钟用初等方法推球的表面积公式 顺手牵一下球的体积公式 哔哩哔哩

電卓の使い方 表面積を求める球の半径を入力して「計算」ボタンを押してください。 円周率は変更できます。 円周率で「πを使う」にチェックを入れると円周率をπとして計算します。 表面積を球の表面積や体積は円錐や円柱と比べたとき、特別な関係にあります。 球の表面積は、その球がぴったり入る円柱の側面積と等しい 同じ高さの場合、円錐：球：円柱の体積比は1：2：3 これらにそれでは、問題を通して球の公式をしっかりと身につけていきましょう！ 半径6㎝の球の体積、表面積をそれぞれ求めなさい。 解説＆答えはこちら 次の図形の体積、表面積をそれぞれ求めなさい

14 平面及立體圖形 立體圖形的表面積及體積 齊齊溫

Scipy5 01 积分应用 椭球体积的数值积分计算 Nutron Ma的博客 Csdn博客 椭球积分求体积

この結果から表面積は \(24a^2\)ということが分かります。 体積が分かれば表面積を計算できるケースがあるということを覚えておきましょう。 球の表面積の計算 それでは先ほど説明した立方体の表楕円体の体積 パラミツと言う世界最大級のフルーツがどれだけの体積になるのか計算してみた。 およそ586リットルと出たので、重さ4050kgに達するのが納得できた。 腎臓の大まかな体積の確体積の求め方 重量の求め方 体積の求め方 立体 体積v 截頭円柱 角すい 球冠 楕円体 楕円環 交叉円柱 中空円柱（管） 截頭角すい 球分 円環 円すい 球 球帯 樽形 重量の求め方

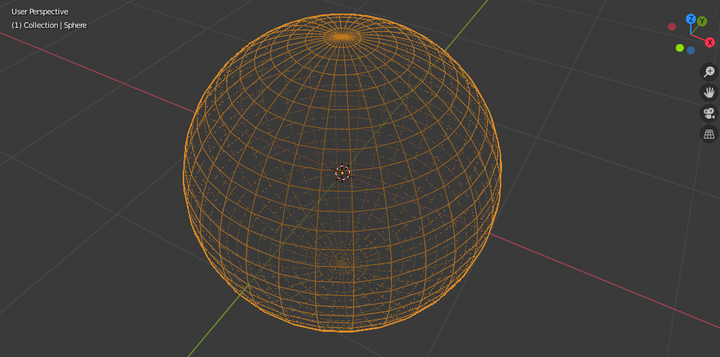
漫谈超球体的体积公式 知乎

球の体積と表面積の公式の覚え方 積分での求め方 高校数学の美しい物語

 ただし、半径 r の n 次元球の体積を V n ( r) と書くことにします。 ・ V 1 ( r) = 2 r ・ V 2 ( r) = π r 2 ・ V 3 ( r) = 4 3 π r 3 3 次元球の体積 V 3 ( r) の公式は中学生で習いますが、積分正八面体の体積、表面積、外接球の半径、内接球の半径 具体例で学ぶ数学 > 図形 > 正八面体の体積、表面積、外接球の半径、内接球の半径 最終更新日 正八面体は、図のような、正三角 「球」の体積・表面積の公式 →練習問題 1 「柱」の体積・表面積の公式 四角柱 三角柱 円柱 柱の体積 = 底面積 × 高さ 表面積 = 底面積 × 2 側面積 円周や側面積とかの求め方も知りた

球の体積と表面積を積分で証明 京大卒が解説 高校数学 テラコヤプラス By Ameba

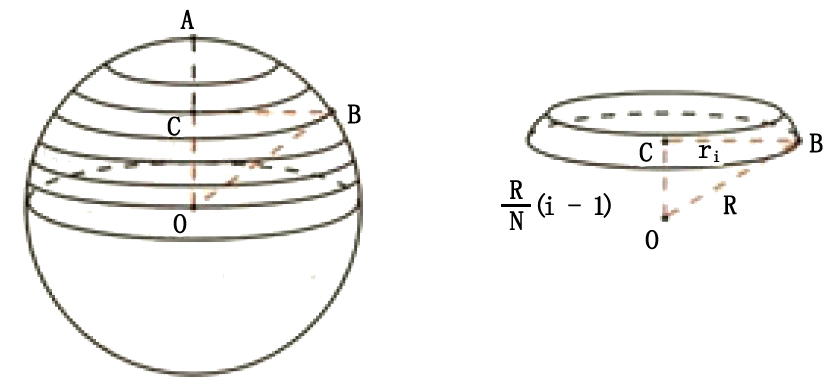
球的体积公式推导 Typecool的博客 Csdn博客 球的体积公式推导过程

球の体積と表面積の公式の覚え方・積分での求め方 の表面積の証明1とほぼ同じことをやるだけです。 証明 もとの球の半径を r r とする。 \Delta\theta Δθ を十分 0 0 に近い正の数として，緯度が 球の表面積は\ (S= 4\pi r^2\) この式を見比べていて、中学生の時の僕は何か規則性があることに気づきました。 円の面積\ (A=\pi r^2\)の式において、\ (r^2\)の\ (2\)を前にかけて、\V = 体積 S = 角錐底面積 角錐台 V = 体積 (角錐台) S1 = 角錐底面積 S2 = 角錐上面積 球体 V = 体積 A = 球体の表面積 r = 球体半径 楕円体 楕円体の体積 → 楕円体 楕円体の表面積 台形 A = 面積 A = 面

写给5年级的学生 球公式是如何推导出来的 表面积

球体表面积和体积公式推导 哔哩哔哩

 球の表面積の求め方には公式があるんだ。 球の半径をrとすると、その表面積は、 4πr^2 になるよ。 つまり、 4 × 円周率 × 半径 × 半径 ってわけだね。 たとえば、半径30cm のサッこれが求める半径1の4次元球体の体積です。 5 「4次元の球」の「表面積」 「4次元の球」の「表面積」の公式を求めてみましょう。 まず、半径がrの「4次元の球」の「4次元的な体積」の公式を出し 下記の記事で、\(n\)次元空間の半径\(R\)の球の体積というのを求めました。 前回の記事はこちら n次元空間における半径Rの球の体積 n次元の球の体積なんて聞いたことないかもしれま

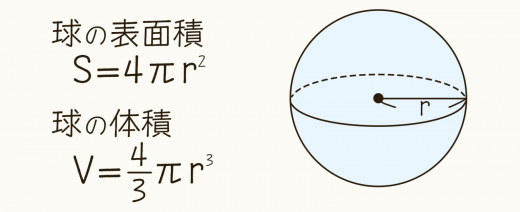
球の体積と表面積の公式の覚え方 積分での求め方 高校数学の美しい物語

椭球的体积公式和表面积公式是什么啊 百度经验

球體表面積 球體表面積是指球面所圍成的幾何體的面積 它包括球面和球面所圍 華人百科

球の体積と表面積の公式をごちゃまぜにしない2つのポイント Qikeru 学びを楽しくわかりやすく

球冠表面积公式 百度百科

球の表面積と体積を求める公式 中学数学 By Okボーイ マナペディア

教案高一数学人教版必修二1 3 2球的表面积和体积 教习网 教案下载

官方双语 为什么球的表面积是同样半径圆的面积的四倍 哔哩哔哩

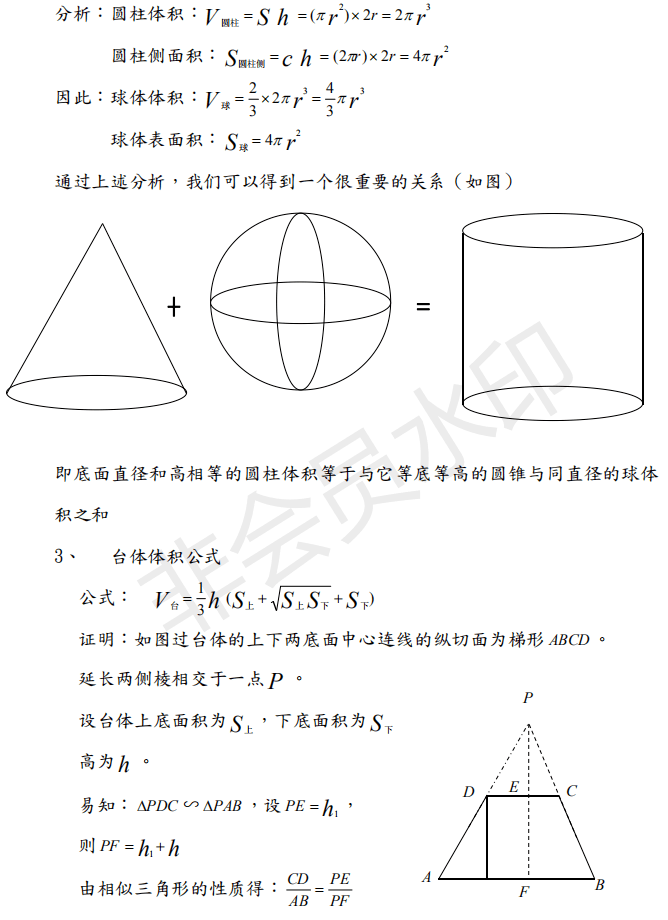
22高三数学第一轮复习 空间几何体的表面积与体积公式大全 整理

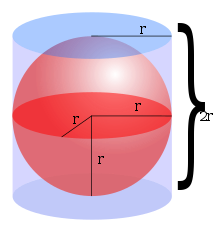
球面 維基百科 自由的百科全書

球の表面積と体積の公式 数学fun

球冠表面积公式 百度百科

圆锥与球与圆柱

球体表面积计算公式 爱问知识人

球の体積と表面積を積分で証明 京大卒が解説 高校数学 テラコヤプラス By Ameba

球の体積と表面積を積分で証明 京大卒が解説 高校数学 テラコヤプラス By Ameba

012 球的体积空间几何体高中数学 Youtube

球体表面积公式 怎样计算球体的表面积

問題 球體體積 數學版 深藍論壇

中１ 数学 球の体積と表面積 Youtube

角錐 円錐の体積と表面積の公式 数学fun

圆台侧面积和体积公式的推导过程 圆台体积公式和表面积 腾讯云开发者社区 腾讯云

求球体的表面积和体积 Xiuye Xy的博客 Csdn博客

球的表面积公式和体积公式是什么 知识问答 少儿教育加盟网

球の表面積と体積の公式 数学fun

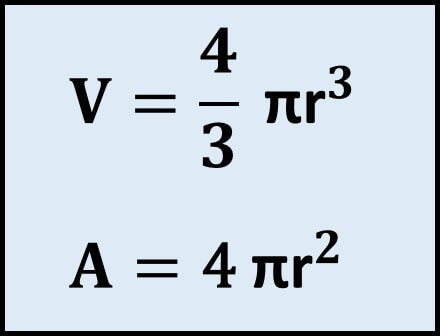
球體表面積 體積計算器 輸入數值自動計算 Lazyorangelife

球的表面積的求法 中學數學課 隨意窩xuite日誌

球の体積公式の微分が表面積になっている理由 Youtube

球的表面积公式和体积公式是什么 知识问答 少儿教育加盟网

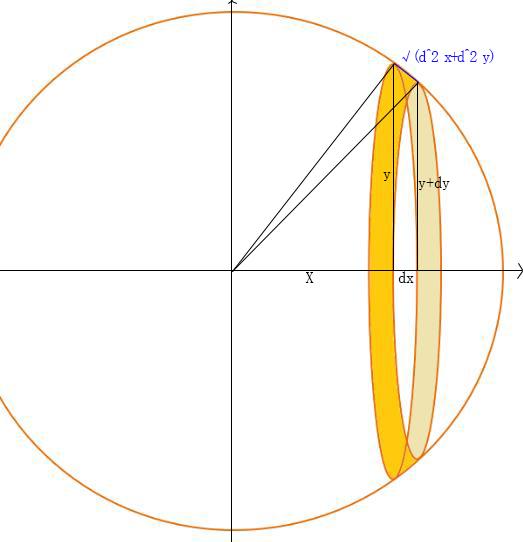
用积分推导球的表面积有哪些方法

球の表面積の求め方 中学生の子に公式の覚え方のコツを紹介 中学や高校の数学の計算問題

認識圓錐 圓錐表面積 體積怎麼算 統整計算公式 實例解題amazingtalker

球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ

体积公式 百度百科

球的体积公式的推导 Zhangjin11的博客 Csdn博客 球的体积公式推导过程

球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ

球の体積 表面積 実験から公式を 授業実践記録 アーカイブ一覧 数学 高等学校 知が啓く 教科書の啓林館

球體的體積及表面面積 哔哩哔哩

球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ

在球的体积公式中 为什么会出现三分之四这个奇怪的

球帽球体积球楔比表面积 点公式png图片素材免费下载 图片编号 Png素材网

球表面积公式推导图解 搜狗图片搜索

球的表面积与体积公式 搜狗图片搜索

球の体積と表面積を積分で証明 京大卒が解説 高校数学 テラコヤプラス By Ameba

涨分 高中数学 空间几何表面积与体积公式大全 背会高考必胜 手机搜狐网

计算球体积和球表面积 Chenjin555的博客 Csdn博客 球体表面积计算公式

球冠体积 表面积在线计算器

球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ

球缺 维基百科 自由的百科全书

Q Tbn And9gcs5vpyjueqh6qhoq0stxl2kb1r8hghvs656c8rpp6r6teufdqdhpe Usqp Cau

球的體積的求法 中學數學課 隨意窩xuite日誌

常用体积计算公式 电子发烧友网

中学数学 球の表面積の求め方の公式を1発で覚える方法 Qikeru 学びを楽しくわかりやすく

用感覺理解球體表面積公式 Youtube

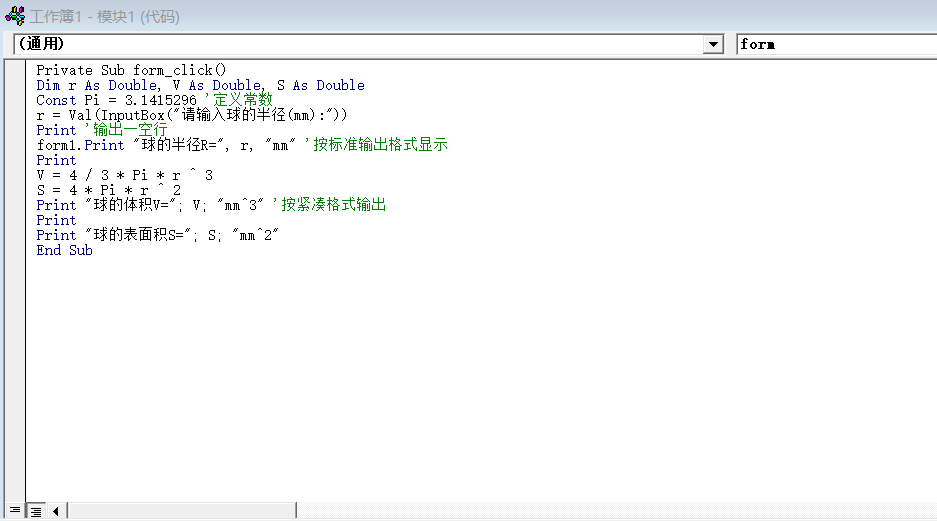
Vb实验 计算球的体积与表面积 隔壁老王521的博客 Csdn博客

Q Tbn And9gcr0 8hqr2ybsj9uwmxjqzp1xxfdm7cwg8bqpqhrrs7hhgcnpl9 8qq7 Usqp Cau

球の表面積と体積の公式 数学fun

球表面积推导过程 球表面积推导过程二重积分 球表面积推导过程图 抖音

1 6 球的表面積與體積 Mathtsing高中數學 Youtube

球体表面积 百度百科

Hkdse 數學練習平台 立方體其實都係prism 所以體積公式都係v Bh Facebook

球の体積 表面積 公式の覚え方は語呂合わせで 問題を使って解説 数スタ

科學月刊 大小有什麼差別 上

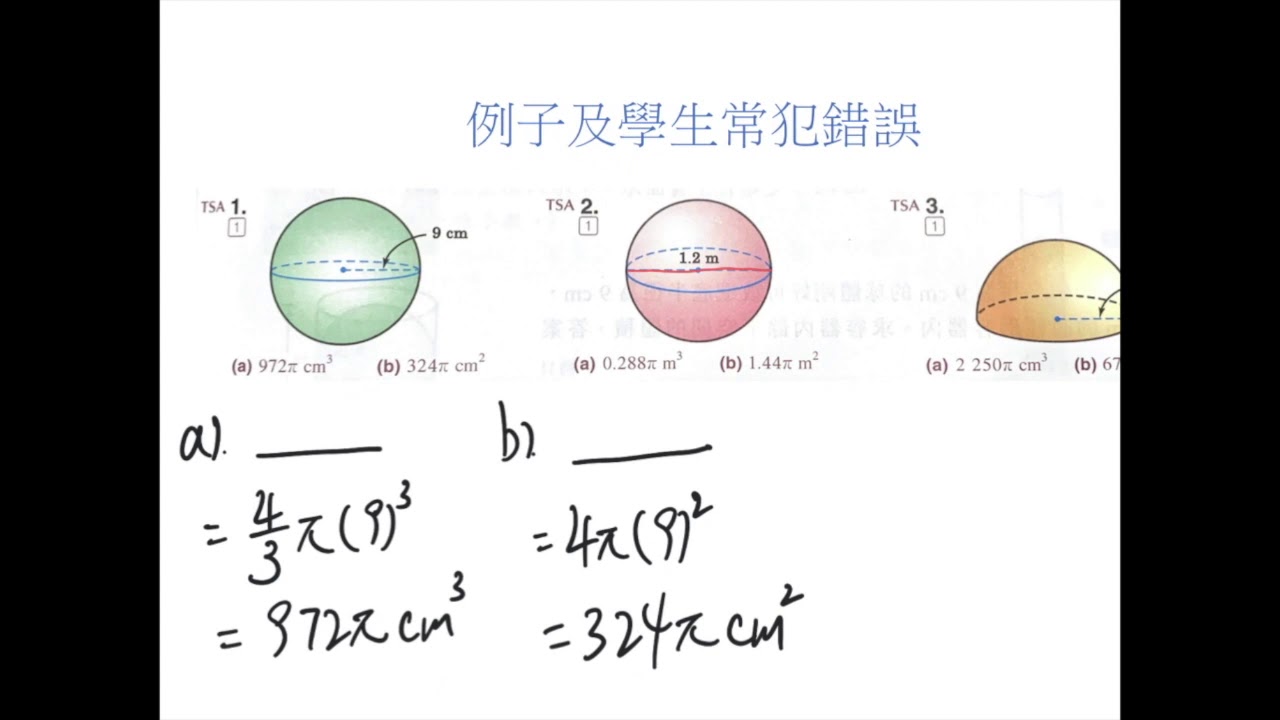
球體體積 總表面面積 Youtube

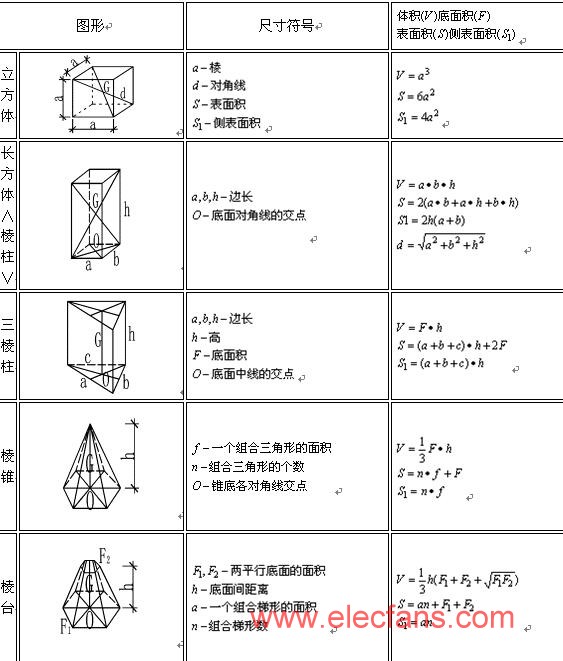
常用体积计算公式 电子发烧友网

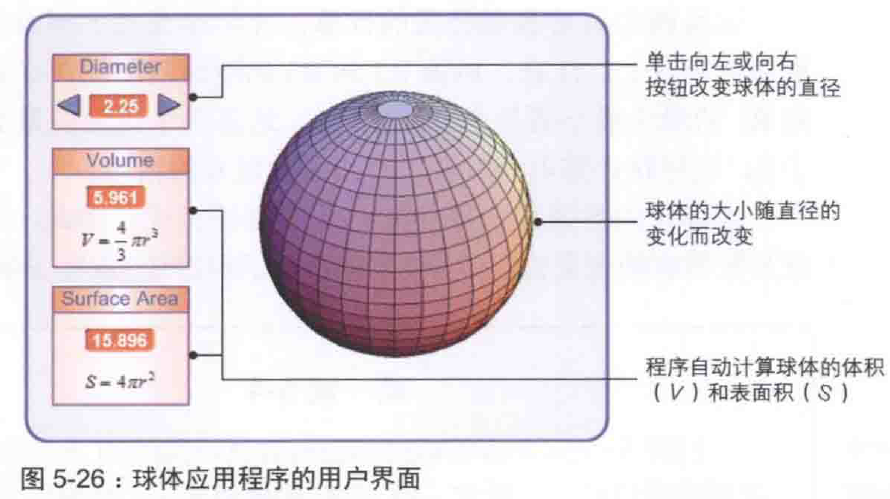
Scratch3 0计算球体体积和表面积 有间学堂 博客园

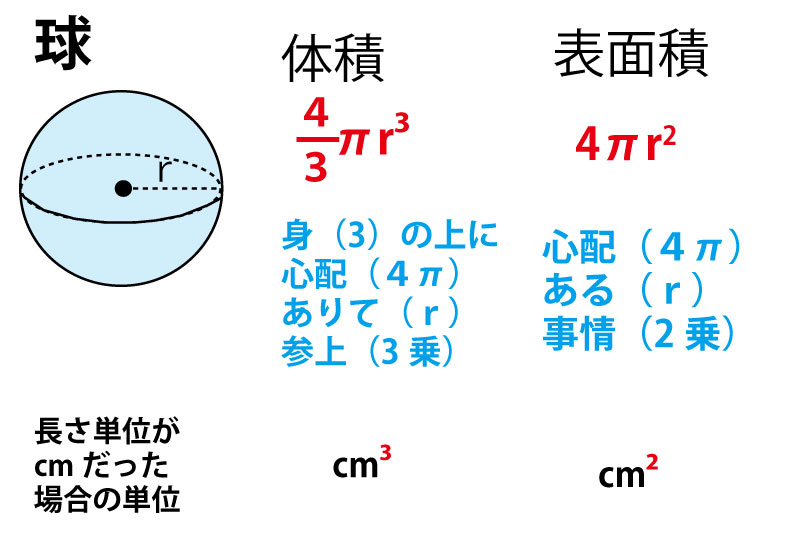
16年前期 千葉県公立高校入試 数学 第2問 1 球の体積 表面積 解答 解説 船橋市議会議員 朝倉幹晴公式サイト

球体计算器 球体体积计算 球体表面积计算 球体直径计算 球体周长计算

證明球體體積公式 Youtube

Q Tbn And9gcsz1hgddt97p4he2m1bxfhidfntduo0 3xhkspillrokhrinwolh71k Usqp Cau

圆球表面积公式用微积分如何推导 知乎

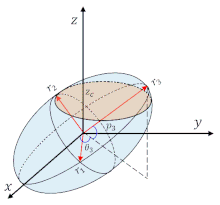
橢球 維基百科 自由的百科全書

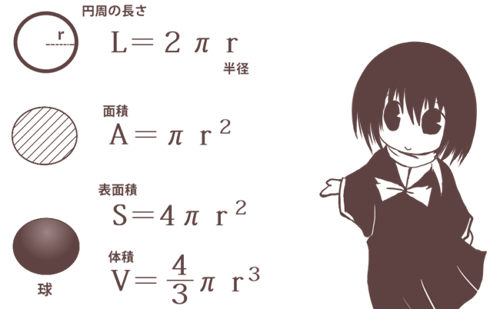
球に関する公式 理数系学習サイト Kori

球の体積と球の表面積の公式 求め方 証明や計算問題も解説 受験辞典

求球体表面积体积已知半径 Onestopweb 博客园

涨分 高中数学 空间几何表面积与体积公式大全 背会高考必胜 都用

表面积体积公式大全 搜狗图片搜索

常用体积计算公式 电子工程世界

球の体積と表面積の公式と覚え方を一目でわかるように図を用いて解説します 練習問題付き 高校生向け受験応援メディア 受験のミカタ

球体表面积 数学术语 搜狗百科

球の体積と球の表面積の公式 求め方 証明や計算問題も解説 受験辞典

球的表面积公式是怎么推导出来的 Zhangjin11的博客 Csdn博客 球的表面积公式怎么推导出来的

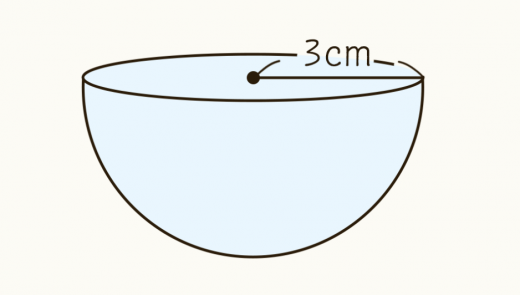
球の体積と表面積の公式の覚え方 積分での求め方 高校数学の美しい物語

Q Tbn And9gcq7htuu4diqo Lkr6xz0 Dqz8w3560qa10gwnvneh74nehy33vsnvk8 Usqp Cau

球的体积公式 搜狗图片搜索

球冠计算器 在线查询计算工具

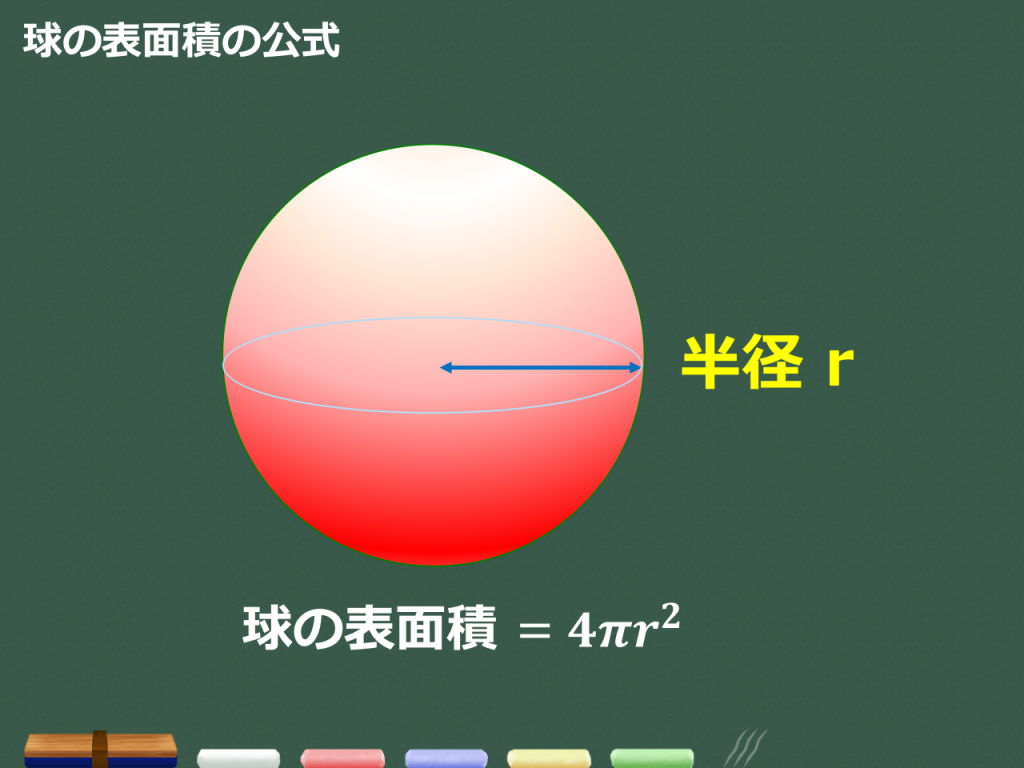
3分で分かる 球の体積と表面積の公式 覚え方 語呂合わせ についてわかりやすく 合格サプリ

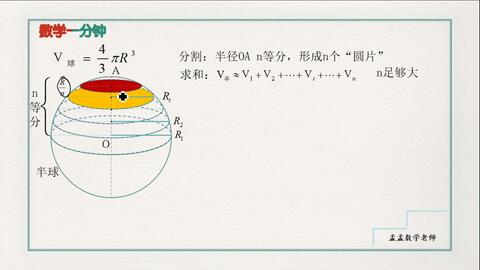
数学一分钟球的体积公式推导证明 哔哩哔哩

在球的体积公式中 为什么会出现三分之四这个奇怪的系数 体积 公式 系数 新浪新闻

圆的表面积体积公式 爱问知识人

椭球表面积公式 搜狗图片搜索

球の体積と表面積を積分で証明 京大卒が解説 高校数学 テラコヤプラス By Ameba

Incoming Term: 球体 表面積 体積 公式,